国债期货的价格计算核心在于“转换因子”和“最便宜可交割券”这两个概念,它不像股票期货那样简单,因为国债期货的标的资产是一个虚拟的“标准券”,而实际交割的是市场上真实存在的各种国债。

下面我们分步拆解这个过程。
核心概念:转换因子
转换因子 是连接虚拟的“标准券”和市场上真实可交割国债的桥梁,它衡量的是,面值为1元的某只可交割国债,在期货合约到期日,其剩余现金流的价值。
转换因子的作用:
- 标准化: 将不同期限、不同票面利率的国债,都“转换”成期货合约所定义的“标准国债”的价值。
- 定价基准: 期货的理论价格是基于某个“标准券”的,而转换因子让其他所有可交割券都能与这个基准进行比较。
转换因子的计算公式:
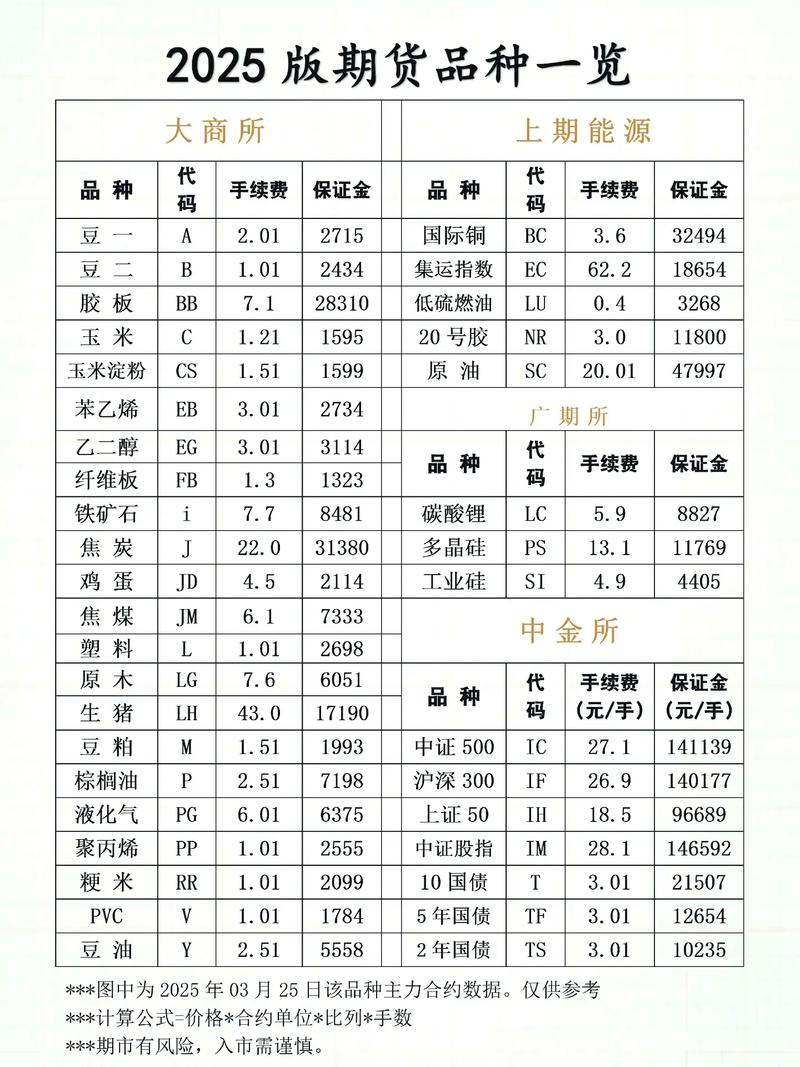
计算转换因子需要一些假设条件:
- 交割日: 假设为合约月份的第一个自然日(但实际上交割有一个月的时间窗口)。
- 利率: 假设一个 flat yield curve(平坦的收益率曲线),且这个收益率就等于该期货合约的“名义标准券”的票面利率,对于中国5年期国债期货,这个票面利率通常是3%;对于10年期,是3%。
公式如下:
$$ CF = \frac{1}{(1 + r)^{\frac{x}{12}}} \times \left[ \frac{C}{r} + \frac{1 - \frac{1}{(1 + r)^n}}{r} \right] - \frac{C}{r} \times \left[ 1 - \frac{x}{12} \right] $$
公式参数解释:

CF: 转换因子C: 可交割国债的年票面利率(一只票面利率为2.6%的国债,C=0.026)r: 假设的年贴现率(即期货合约的“名义标准券”票面利率,如5年期为0.03)n: 从交割日到国债到期日所剩余的完整付息年数(包括下一个付息周期)。x: 从当前付息日到交割日之间的月份数(0 < x ≤ 6)。
简化理解:
这个公式的本质是,将国债未来的所有现金流(票息和本金)用假定的收益率 r 贴现到交割日,然后将其价值标准化为面值为1元的现值。
核心概念:最便宜可交割券
在交割日,空方(卖方)可以从所有符合交割标准的国债中,选择对自己最有利(成本最低)的一只进行交割,这只国债就是最便宜可交割券。
如何确定CTD? 空方交割一只国债,其成本是这只国债的现货市场价格,而他能从多方(买方)那里获得的收入是期货价格 × 转换因子 + 应计利息。
空方会选择使 “买入成本 - 交割收入” 最小化的国债。
CTD的判断公式: 我们通常用隐含回购利率 来判断CTD,IRR是衡量通过“买入现货国债、同时卖出期货合约”这一套利策略所能获得的年化收益率。IRR最高的那只国债,就是CTD。
IRR的计算思路:
- 现金流出: 在当前时点,买入一只可交割国债,花费其全价(净价 + 应计利息)。
- 现金流入: 在期货交割日,交割这只国债,获得
期货价格 × 转换因子 + 交割日当天的应计利息。 - IRR: 求解使得未来现金流入的现值等于当前现金流出的那个内部收益率。
在实际操作中,交易员和计算机会遍历所有可交割券,计算每只的IRR,IRR最高的那一只就是当前的CTD。
国债期货的理论价格计算公式
在确定了CTD之后,国债期货的理论价格就可以通过“无套利定价原理”来推导,其核心思想是:持有CTD现货的成本,应该等于持有期货合约的成本。
持有成本模型
$$ F{理论} = \frac{(S{CTD} + AI_0) \times (1 + r \times \frac{T}{360}) - AIT}{CF{CTD}} $$
公式参数解释:
F_理论: 国债期货的理论价格S_CTD: CTD国债的当前净价。(注意:不是全价)AI_0: 从当前日到交割日,CTD国债的应计利息。r: 无风险资金利率(如回购利率,代表持有国债的资金成本)。T: 从当前日到交割日的天数。AI_T: 在交割日当天,CTD国债的应计利息(通常为0,因为交割日一般就在付息日之后)。CF_CTD: CTD国债的转换因子。
公式简化与逻辑拆解
这个公式可以更直观地理解为:
$$ F_{理论} = \frac{\text{CTD国债在交割日的全价}}{\text{CTD国债的转换因子}} $$
而CTD国债在交割日的全价,可以通过其当前全价加上持有成本来计算:
- 当前全价:
S_CTD + AI_0(净价 + 当前应计利息) - 持有成本:
(S_CTD + AI_0) * r * (T/360)(持有期间的资金成本) - 交割日全价:
(S_CTD + AI_0) * (1 + r * T/360) - AI_T(在交割日,上一个付息周期的利息已经支付,所以要减去AI_T)
将这个交割日的全价,除以转换因子 CF_CTD,就得到了对应期货合约的理论价格。
举例说明(简化版)
假设我们有一个5年期国债期货,其“名义标准券”票面利率为3%。
市场情况:
- 可交割国债A:
- 票面利率: 2.6%
- 当前净价: 99.50元
- 转换因子: 0.9850
- 距下次付息还有3个月
- 可交割国债B:
- 票面利率: 3.5%
- 当前净价: 101.20元
- 转换因子: 1.0120
- 距下次付息还有3个月
- 资金成本: 2.5% (年化)
- 距离交割: 90天
步骤1:计算应计利息 (简化计算,假设按单利)
AI_0(A和B都一样) = (票面利率 / 2) (3/12) = (0.026 / 2) 0.25 = 0.00325元 (对于A券)AI_0(B券) = (0.035 / 2) * 0.25 = 0.004375元 (对于B券)
步骤2:计算交割日全价
- A券交割日全价 = (99.50 + 0.00325) (1 + 0.025 90/360) - 0 = 99.50325 * 1.00625 ≈ 100.125元
- B券交割日全价 = (101.20 + 0.004375) (1 + 0.025 90/360) - 0 = 101.204375 * 1.00625 ≈ 101.830元
步骤3:计算期货理论价格
- 基于A券的理论价 = 100.125 / 0.9850 ≈ 65元
- 基于B券的理论价 = 101.830 / 1.0120 ≈ 62元
在这个例子中,基于国债B计算出的理论价格(100.62元)更低,这意味着,如果期货市场价格高于100.62元,做空者选择B券交割更有利。国债B是更便宜的交割券,期货的理论价格应该由它决定,即65元是一个错误的理解,正确的应该是62元,这个例子也说明了,转换因子高的国债(B券),其净价也必须足够低,才能成为CTD。
| 概念 | 作用 | 计算关键 |
|---|---|---|
| 转换因子 | 将不同国债标准化为“标准券” | 用期货名义票息率贴现未来现金流 |
| 最便宜交割券 | 空方会选择对自己最有利的国债进行交割 | 计算各券的隐含回购利率,IRR最高者为CTD |
| 期货理论价格 | 基于无套利原则推导出的公允价格 | F = (CTD交割日全价) / CTD转换因子 |
在实际交易中,由于市场利率、CTD等因素会不断变化,期货价格会围绕理论价格上下波动,为投资者提供了套利和交易的机会。
标签: 国债期货定价公式详解 国债期货价格计算方法 如何计算国债期货理论价格